[toc]

Array

  • The memory addresses of array elements are contiguous.

  • Contiguous Memory Addresses of 2D Arrays

    Memory management differs across programming languages.

    • C++ 2D Array:

      • Contiguous memory allocation.
      • Efficient for accessing elements in row-major order.

    • Java 2D Array:

      • 像Java是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。

        所以看不到每个元素的地址情况

      • Non-contiguous memory allocation.

      • Each row is a distinct array object, leading to potential memory fragmentation.

      • Offers flexibility in handling rows of varying lengths (jagged arrays).

Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

1
2
3
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

✨

Understanding Interval Rules:

  • Inclusive-exclusive rule: The search interval is [left, right) where left is inclusive and right is exclusive.
  • Inclusive-inclusive rule: The search interval is [left, right] where both left and right are inclusive.
  • Understand how to correctly calculate mid based on these interval rules.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int search(int[] nums, int target) {
       int left = 0;
       int right = nums.length - 1;
       while(left <= right){
            int mid = (left + right)/2;
            if(nums[mid] == target) return mid;
            if(nums[mid] > target){
                right = mid - 1;
            }else{
                left = mid + 1;
            }
       } 
       return -1;
    }
}

35. Search Insert Position

Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

1
2
Input: nums = [1,3,5,6], target = 5
Output: 2

Example 2:

1
2
Input: nums = [1,3,5,6], target = 2
Output: 1

Example 3:

1
2
Input: nums = [1,3,5,6], target = 7
Output: 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int searchInsert(int[] nums, int target) {
        
        int left = 0 ; 
        int right = nums.length - 1;

        if(target < nums[0]) return 0;
        if(target > nums[right]) return right + 1;

        while(left <= right){
            
            int mid = (right + left)/2;
            //int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] > target){
                right = mid - 1;
            }else{
               left = mid + 1;
            }
        }
        return left; // not return right;
    }
}

34. Find First and Last Position of Element in Sorted Array

Medium

Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.

If target is not found in the array, return [-1, -1].

You must write an algorithm with O(log n) runtime complexity.

Example 1:

1
2
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

Example 2:

1
2
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

Example 3:

1
2
Input: nums = [], target = 0
Output: [-1,-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0 ; 
        int right = nums.length - 1;
        // if(nums.length == 1){
        //     if(nums[0] == target)  return new int[]{0, 0};
        //      return new int[]{-1, -1};
        // }
        // if(nums.length < 1 || target < nums[0] ||target > nums[right] ) return new int[]{-1, -1};
		// dont need those no more
        
        while(left <= right){
            
            int mid = (right + left)/2;
            //int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                int mleft = mid;
                int mright = mid;
                while(mleft >= 0 && nums[mleft] == nums[mid] ) mleft --; //! mleft >= 0
                while(mright < nums.length && nums[mright] == nums[mid] ) mright ++; //! mright < nums.length
                return new int[]{mleft+1, mright-1};
            }else if(nums[mid] > target){
                right = mid - 1;
            }else{
               left = mid + 1;
            }
        }
        return new int[]{-1, -1};
    }
}

27. Remove Element

Input: nums = [3,2,2,3], val = 3
Output: 2, nums = [2,2,,]
Explanation: Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).

✨

two pointers

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int removeElement(int[] nums, int val) {
        int flag = 0;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] != val){
                nums[flag] = nums[i];
                flag ++;
            }
        }
        return flag;
    }
}
// flag   is slowIndex
// i      is fastIndex

977. Squares of a Sorted Array

Given an integer array nums sorted in non-decreasing order, return an array of the squares of each number sorted in non-decreasing order.

Example 1:

1
2
3
4
Input: nums = [-4,-1,0,3,10]
Output: [0,1,9,16,100]
Explanation: After squaring, the array becomes [16,1,0,9,100].
After sorting, it becomes [0,1,9,16,100].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// O(nlogn)
class Solution {
    public int[] sortedSquares(int[] nums) {
        for(int i = 0 ; i < nums.length; i++){
            nums[i] = nums[i] * nums[i];
        }
        Arrays.sort(nums);
        return nums;
    }
}

//  O(n)
// two pointers
class Solution {
    public int[] sortedSquares(int[] nums) {
        int[] res = new int[nums.length];
        int index = nums.length - 1;
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){
            int left2 = nums[left] * nums[left];
            int right2 = nums[right] * nums[right];
            if(left2 >= right2){
                res[index] = left2;
                left ++;
            }else{
                res[index] = right2;
                right --;
            }
            index --;
        }
        return res;
    }
}

✨

two pointers:

The maximum value of the squares of the array elements will be at either end of the array, either the leftmost or the rightmost element, and it cannot be in the middle.

img

209. Minimum Size Subarray Sum

Medium

Given an array of positive integers nums and a positive integer target, return the minimal length of a

subarray

whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.

✨ subarray is continuous. can’t change the index order.

Example 1:

1
2
3
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// sliding window
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0; 
        int right = 0;
        int  min = Integer.MAX_VALUE;
        int sum = 0;
        for(int i = 0 ; i < nums.length; i++){ 
            right = i;
            sum += nums[right];
            while(sum >= target){
                min = Math.min(min, right - left + 1);
                sum -= nums[left];
                left ++;
            }
        }
        return (min == Integer.MAX_VALUE? 0 : min);
    }
}

  • Let’s walk through the process of finding the minimum size subarray sum that exceeds the target sum 7 for the array [2, 3, 1, 2, 4, 3].

    209.长度最小的子数组

  • Sliding Window Technique:

    • Involves using a window (often defined by two pointers) to solve array or sequence-related problems.
    • Utilizes the window to perform operations or find solutions.
    • Can be considered an application of the two pointers technique, as it often involves moving two pointers to define and slide the window.

  • Two Pointers Technique:

    • Involves using two pointers to traverse an array or sequence, typically towards each other.
    • Used to find pairs or subsequences that satisfy certain conditions.
    • May not always involve defining a window, unlike the sliding window technique.

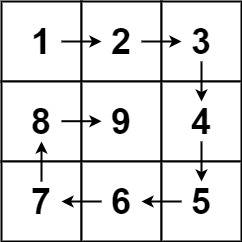
59. Spiral Matrix II

Medium

Given a positive integer n, generate an n x n matrix filled with elements from 1 to n2 in spiral order.

Example 1:

img

1
2
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[][] generateMatrix(int n) {
        int side = n;
        int[][] res = new int[side][side];
        int num = 1;
        for(int i = 0 ; i < side/2; i++){ //layer outter -> inner
            //top
            for(int y = i ; y < side - 1 - i ; y++){
                res[i][y] = num++;
            }
            //right
            for(int x = i  ; x < side - 1 - i ; x++){
                res[x][side - 1 - i ] = num++;
            }
            //bottom
            for(int  y = side - 1 - i  ; y > i; y--){
                res[side - 1 - i ][y] = num++;
            }
            //left
            for(int x = side - 1 - i ; x > i; x--){
                res[x][i] = num++;
            }
        }
        if( n % 2 == 1){
            res[n/2][n/2] = num;
        }
        return res;
    }
}

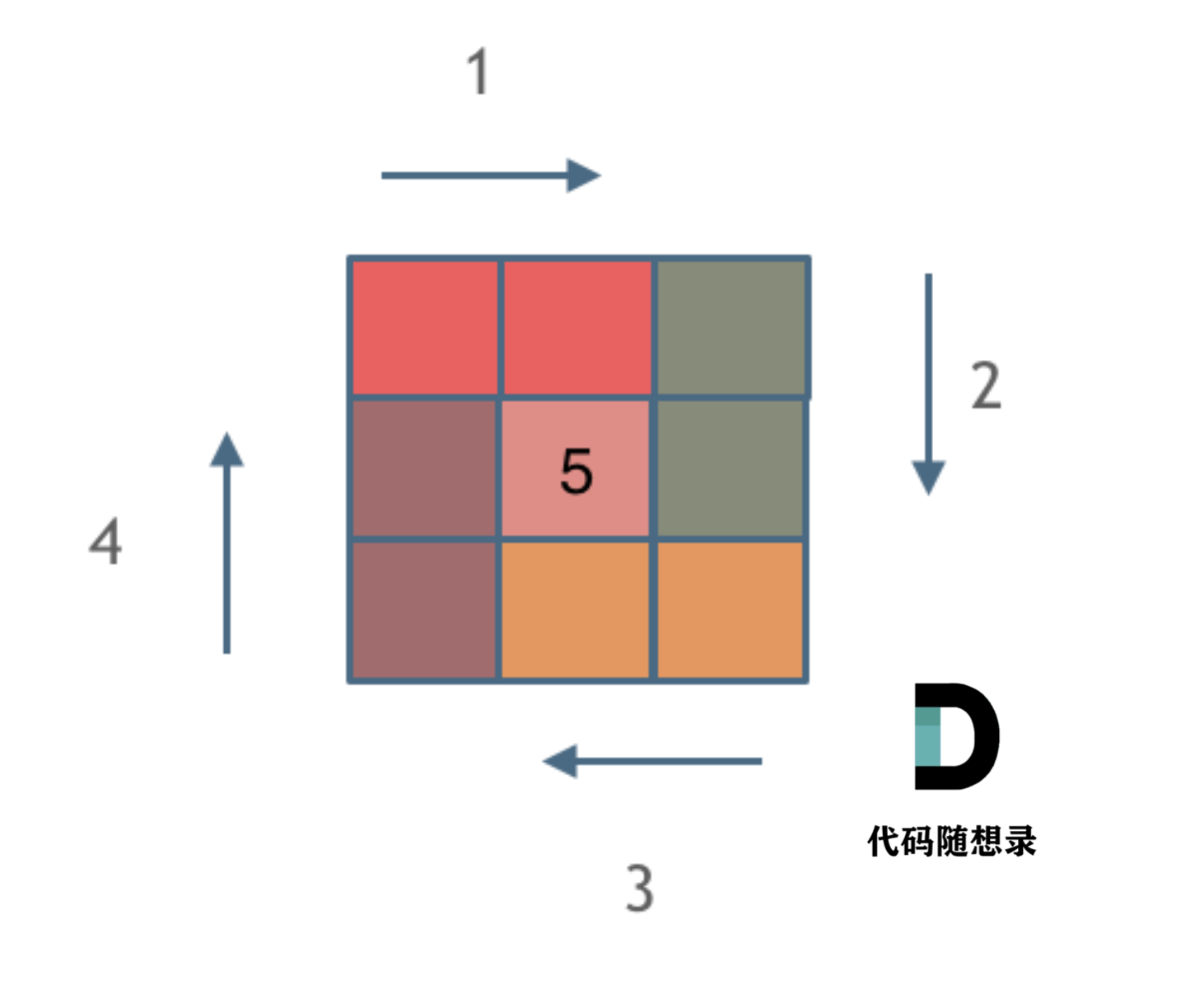
✨模拟转圈

Pay attention to boundary issues.

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

So, following the left-closed and right-open principle, let me draw a circle.

img

这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。