DP🌼

Summarize:

What’s DP?

You break down the problem into smaller subproblems. The solution to the original problem can then be constructed from the solutions of its subproblems. 重叠子问题

Dynamic Programming Five Steps:

Here, we’ll use a one-dimensional DP array to store the results of recursion.

Determine the meaning of the DP array and its indices:

The meaning of dp[i] is:
Establish the recurrence relation:

dp[i] = dp[i - 1] + dp[i - 2].
Initialize the DP array:

dp[0] = 0; dp[1] = 1;
Determine the traversal order:

From the recurrence formula dp[i] = dp[i - 1] + dp[i - 2], it’s evident that dp[i] depends on dp[i - 1] and dp[i - 2], so the traversal order must be from front to back.

1. Fundamental questions

climbing stairs

70. Climbing Stairs

dp[i]: There are dp[i] ways to climb to the i-th stair.

746. Min Cost Climbing Stairs

The definition of dp[i]: the minimum energy spent to reach the i-th step is represented by dp[i].

62. Unique Paths

dp[i] [j]: Represents the number of different paths from (0, 0) to (i, j).
notice its the number of different paths not steps

```
for (int i = 0; i < m; i++) dp[i][0] = 1; //not i
for (int j = 0; j < n; j++) dp[0][j] = 1;


dp[i] [j] = dp[i - 1] [j] + dp[i] j - 1]

[63. Unique Paths II](https://leetcode.com/problems/unique-paths-ii/)

Question 63, compared to Question 62, presents an additional challenge of obstacles.

! [343. Integer Break](https://leetcode.com/problems/integer-break/)

dp[i]: The maximum product obtained by breaking the number i into factors is dp[i].

* dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

**this is important :**
dp[i] = Math.max(dp[i], Math.max(dp[i-j]*j,* j*(i-j)  ));

dp[i-j]*j -> 至少是三个integer相乘

j*(i-j) -> 两个integer相乘

* j <= i/2

[96. Unique Binary Search Trees](https://leetcode.com/problems/unique-binary-search-trees/)!

* **dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]**。

  也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ，都是一样的。

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量  !!!!!!!!!!!!!别忘了这步，最后全部相加，不要光去乘

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

* dp[i] += dp[j - 1] * dp[i - j] 

  not dp[i] += dp[j ] * dp[i - j]

### 2.0/1 knapsack problem  

* **<font style="color : red"> [summary](https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.md) two dimension array </font>**

**dp[i] [j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少**。

// initialization

for (int j = 0 ; j < weight[0]; j++) { // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}




```java
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    dp[i][j] = dp[i-1][j];
                } else {
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]); 
                    //notice, not dp[i][j-1]
                }
            }
        }

summary one dimension array

在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

初始化都是零

//wrong versuin:
for (int i = 1; i < weight.length; i++) {
        for (int j = 1; j <= bagSize; j++) {
            if(j > weight[i]){
                dp[j] = Math.max(dp[j - weight[i]] + value[i], dp[j-1] );
             }else{
                dp[j] =  dp[j-1];
             }
        }
    }
//right:
//遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 0; i < wLen; i++){
            for (int j = bagWeight; j >= weight[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); // notice its not dp[j-1]
            }
        }

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

初始化都是零

weight[1, 1, 2]
value[10, 15, 40]

-----------------------j: 0 -> capacity:
i=0
dp[1] = dp[1 - weight[0]] + value[0] = dp[0] + 10 = 10
dp[2] = dp[2 - weight[0]] + value[0] = dp[1] + 10 = 20
dp[3] = dp[3 - weight[0]] + value[0] = dp[2] + 10 = 30
i=1
dp[1] = dp[1 - weight[1]] + value[1] = dp[0] + 15 = 15
dp[2] = dp[2 - weight[1]] + value[1] = dp[1] + 15 = 25
dp[3] = dp[3 - weight[1]] + value[1] = dp[2] + 15 = 35


------------------------j: capacity -> 0
i = 0
dp[3] = dp[3 - weight[0]] + value[0] = dp[2] + 10 = 10
dp[2] = dp[2 - weight[0]] + value[0] = dp[1] + 10 = 10
dp[1] = dp[1 - weight[0]] + value[0] = dp[0] + 10 = 10 
i = 1
dp[3] = dp[3 - weight[1]] + value[1] = dp[2] + 15 = 35 //覆盖的是上一层的循环结果
dp[2] = dp[2 - weight[1]] + value[1] = dp[1] + 15 = 25
dp[1] = dp[1 - weight[1]] + value[1] = dp[0] + 15 = 15
i = 2
dp[3] = dp[3 - weight[2]] + value[2] = dp[1] + 40 = 55
dp[2] = dp[2 - weight[2]] + value[2] = dp[0] + 40 = 40
dp[1] = dp[1 - weight[2]] + value[2] = dp[-1] + 40 game over haha

416. Partition Equal Subset Sum

Recognizing this problem as a variant of the knapsack problem is crucial.

1049. Last Stone Weight II

Recognizing this problem as a variant of the knapsack problem is crucial.

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。

494. Target Sum!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!———————————-

answer

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = target

x = (target + sum) / 2

此时问题就转化为，装满容量为x的背包，有几种方法。

这里的x，就是bagSize，也就是我们后面要求的背包容量。

大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。

这么担心就对了，例如sum 是5，S是2的话其实就是无解的，所以：

1 2	（C++代码中，输入的S 就是题目描述的 target） if ((S + sum) % 2 == 1) return 0; // 此时没有方案

同时如果 S的绝对值已经大于sum，那么也是没有方案的。

1 2	（C++代码中，输入的S 就是题目描述的 target） if (abs(S) > sum) return 0; // 此时没有方案

再回归到01背包问题，为什么是01背包呢？

因为每个物品（题目中的1）只用一次！

这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来

1	dp[j] += dp[j - nums[i]]

474. Ones and Zeroes

The question is about the 0/1 knapsack problem rather than the unbounded knapsack problem.

okay, first, the definition of dpi j is kind of tricky!!!!!**dp[i] [j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]**。

dp[i] [j] = max(dp[i] [j], dp[i - zeroNum] [j - oneNum] + 1);

以输入：[“10”,”0001”,”111001”,”1”,”0”]，m = 3，n = 3为例

最后dp数组的状态如下所示：

summary

不少同学刷过这道题，可能没有总结这究竟是什么背包。

此时我们讲解了0-1背包的多种应用，

纯 0 - 1 背包是求给定背包容量装满背包的最大价值是多少。
416. 分割等和子集是求给定背包容量，能不能装满这个背包。
1049. 最后一块石头的重量 II 是求给定背包容量，尽可能装，最多能装多少
494. 目标和是求给定背包容量，装满背包有多少种方法。
本题是求给定背包容量，装满背包最多有多少个物品。

所以在代码随想录中所列举的题目，都是 0-1背包不同维度上的应用，大家可以细心体会！

3. “House Robber” series

The progression from “House Robber” to “House Robber II” and then to “House Robber III” on LeetCode essentially extends the problem from a linear sequence to a circular sequence and finally to a tree structure.

198. House Robber

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序

dp[i] = Math.max(dp[i-1], dp[i-2] + value[i]);

213. House Robber II

take the max one between

i : 0 -> len-1

1 -> len

337. House Robber III !!!!!!!!!!!!!!

// Not robbing: Max(Left child not robbing, Left child robbing) + Max(Right child not robbing, Right child robbing)

// Robbing: Left child not robbing + Right child not robbing + Current node robbing

// Index 0 (dp[0]): Not robbing, Index 1: Robbing

确定递归函数的参数和返回值
确定终止条件
确定遍历顺序
确定单层递归的逻辑

I feel like the structure of this answer looks similar to backtracking problem.

4. stock problem

121. Best Time to Buy and Sell Stock

//dp[i][0] represents the maximum cash obtained from holding stocks on the i-th day.
// dp[i][1] represents the maximum cash obtained from not holding stocks on the i-th day.
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

Sample question:

322. Coin Change

可重复Return the fewest number of coins that you need to make up that amount.

class Solution {
    public int coinChange(int[] coins, int amount) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[amount + 1];
        //初始化dp数组为最大值
        for (int j = 0; j < dp.length; j++) {
            dp[j] = max;
        }
        //当金额为0时需要的硬币数目为0
        dp[0] = 0;
        for (int i = 0; i < coins.length; i++) {
            //正序遍历：完全背包每个硬币可以选择多次
            for (int j = coins[i]; j <= amount; j++) {
                //只有dp[j-coins[i]]不是初始最大值时，该位才有选择的必要
                if (dp[j - coins[i]] != max) {
                    //选择硬币数目最小的情况
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        return dp[amount] == max ? -1 : dp[amount];
    }
}

518. Coin Change II

可重复Return the number of combinations that make up that amount.

class Solution {
    public int change(int amount, int[] coins) {
        //递推表达式
        int[] dp = new int[amount + 1];
        //初始化dp数组，表示金额为0时只有一种情况，也就是什么都不装
        dp[0] = 1;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

377. Combination Sum IV

可重复Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for(int j = 0 ; j <= target; j++){
            for(int i = 0; i < nums.length; i++){
                if(j >= nums[i])
                dp[j] = dp[j] + dp[j - nums[i]];
            }
        }
        return dp[target];
    }
}

494. Target Sum

组合数

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        
        for(int num: nums){
            sum += num;
        }
        //如果target的绝对值大于sum，那么是没有方案的
        if (Math.abs(target) > sum) return 0;
        //如果(target+sum)除以2的余数不为0，也是没有方案的
        if ((target + sum) % 2 == 1) return 0;

        int pack = (sum + target) / 2;
        int[] dp = new int[pack + 1];
       dp[0] = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = pack; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        
        return dp[pack];
    }
}

01背包https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-2.md

完全背包 https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.md

steps:

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

动态规划中dp[j]是由dp[j-weight[i]]推导出来的，然后取max(dp[j], dp[j - weight[i]] + value[i])。

但如果是贪心呢，每次拿物品选一个最大的或者最小的就完事了，和上一个状态没有关系。

所以贪心解决不了动态规划的问题。

我在这里做一个总结：

求组合数：动态规划：518.零钱兑换II 求排列数：动态规划：377. 组合总和 Ⅳ、动态规划：70. 爬楼梯进阶版（完全背包）求最小数：动态规划：322. 零钱兑换、动态规划：279.完全平方数

Leetcode:

509. Fibonacci Number

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

1 2	F(0) = 0, F(1) = 1 F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Example 1:

1
2
3

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

class Solution {
    public int fib(int n) {
        if( n < 2)
            return n;
        int[] dp = new int[ n + 1];  
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2; i < dp.length;i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        
        return dp[n];
    }
}

70. Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

这道题的推导公式是这样得来的：
在到达第n层的上一步，我们只有两个选择，走一步，或者走两步。
如果是走一步，我们需要先通过 f(n-1)种方式到达 n-1 层
如果是走两步，我们需要通过 f(n-2)种方式到达第 n - 2 层
所以综上有 f(n) = f(n-2) + f(n-1)

it’s actually Fibonacci Number

class Solution {
    public int climbStairs(int n) {
    if(n <= 2 ){
        return n;
    }
     int[] dp = new int[n];
     dp[0] = 1;
     dp[1] = 2;
     for(int i = 2; i < dp.length; i++){
         dp[i] = dp[i-1] + dp[i-2];
     }
     return dp[n - 1];   
    }
}

0-1 unbounded knapsack

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        int[] nums = {1, 2};
        dp[0] = 1;
        for(int j = 0; j < n+1; j++){
            for(int i = 0; i < 2; i++){
                if(j >= nums[i])
                    dp[j] = dp[j]+dp[j-nums[i]];
            }
        }
        return dp[n];
    }
}

746. Min Cost Climbing Stairs

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

Example 1:

Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        if(cost.length == 1){
            return cost[0];
        }else if(cost.length == 2){
            return Math.min(cost[0],cost[1]);
        }
        int[] dp = new int[cost.length + 1];
        dp[0] = 0;
        dp[1] = 0;
        for(int i = 2; i < dp.length; i ++){
            dp[i] = Math.min(dp[i-1] + cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[dp.length - 1];
    }
}

62. Unique Paths

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

1 2	Input: m = 3, n = 7 Output: 28

// mine: 
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] d = new int[m][n];
        for(int x= 0; x < m; x++){
            for(int y = 0; y < n; y++){
            ----------
                if( y == 0){
                    if(x==0){
                        d[x][y] = 1;
                    }else{
                        d[x][y] = d[x-1][y];
                    }   
                }else if(x == 0){
                     if(y==0){
                        d[x][y] = 1;
                    }else{
                        d[x][y] = d[x][y-1];
                    } 
                }else{
                    d[x][y] = d[x][y-1]+d[x-1][y];
                }
            ---------    
                
                =========> optimize:
                if( y == 0){
                    d[x][y] = 1;
                }else if(x == 0){
                     d[x][y] = 1;
                }else{
                    d[x][y] = d[x][y-1]+d[x-1][y];
                }
                ==========    
            }
        }
        return d[m-1][n-1];
    }
}

//wrong:
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for(int i = 0 ; i < dp.length; i++){
            for(int j = 1 ; j < dp[i].length; j++){ //wrong
                if(i > 0 && j > 0){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }else if(i > 0  && j == 0){
                    dp[i][j] = dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }

        return dp[m - 1][n - 1];
    }
}

63.Unique Paths II

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The testcases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

// mine:
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int[][] dp = new int[obstacleGrid.length][obstacleGrid[0].length];
        if(obstacleGrid[0][0] ==1){
            return 0;
        }

        for(int i = 0; i < obstacleGrid.length; i++){
            if(obstacleGrid[i][0] == 1){
                 while( i < obstacleGrid.length){
                    dp[i][0] = 0;
                    i++;
                 }
            }else{
                dp[i][0] = 1;
            }
        }
        for(int i = 0; i < obstacleGrid[0].length; i++){
            if(obstacleGrid[0][i] == 1){
                while( i < obstacleGrid[0].length){
                    dp[0][i] = 0;
                    i++;
                 }
            }else{
                dp[0][i] = 1;
            }
        }

        for(int x = 1; x < obstacleGrid.length; x++){
            for(int y = 1; y < obstacleGrid[x].length; y++){
                if(obstacleGrid[x][y] == 1){
                    dp[x][y] = 0;
                }else{
                    dp[x][y] = dp[x-1][y] +dp[x][y-1];
                }
            }
        }

        return dp[obstacleGrid.length-1][obstacleGrid[0].length-1];
    }
}

//leetcodemaster:
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        //如果在起点或终点出现了障碍，直接返回0
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
            return 0;
        }

        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {  // ！！！这样写非常neat
        // 循环条件-> 只要遇到了障碍直接就终止循环
            dp[i][0] = 1;
        }
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
            dp[0][j] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
            }
        }
        return dp[m - 1][n - 1];
    }
}
//second try: wrong
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int[][] dp = new int[obstacleGrid.length][obstacleGrid[0].length];
        for(int i = 0 ; i < obstacleGrid.length; i++){
            if(obstacleGrid[i][0] != 1){
                dp[i][0] = 1;
            }else{
                dp[i][0] = 0; //!!!!!!!!!!!!!!!!!!!!!wrong
                //注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理
            } 
        }

        for(int i = 0 ; i < obstacleGrid[0].length; i++){
            if(obstacleGrid[0][i] != 1){
                dp[0][i] = 1;
            }else{
                dp[0][i] = 0; //!!!!!!!!!!!!!!!!!!!!wrong
            } 
        }

        for(int i = 1 ; i < obstacleGrid.length; i++){
            for(int j = 1; j < obstacleGrid[0].length; j++){
                if(obstacleGrid[i][j] == 1)dp[i][j] = 0;
                else dp[i][j] = dp[i-1][j] + dp[i][j - 1];
            }
        }
        return dp[obstacleGrid.length - 1][obstacleGrid[0].length -1];
    }
}

In Java, when you create a new array of certain data type (e.g., int[], double[], char[], etc.), the elements in the array are initialized to default values based on the data type. For numeric data types (e.g., int, double, float, etc.), the default value is 0.

so actually

for(int i = 0; i < obstacleGrid.length; i++){
    if(obstacleGrid[i][0] == 1){
         while( i < obstacleGrid.length){
            dp[i][0] = 0;    // this is unecessary
            i++;
         }
    }else{
        dp[i][0] = 1;
    }
}

343. Integer Break

Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers.

Return the maximum product you can get.

Example 1:

1
2
3

Input: n = 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.

class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1];
        dp[2] =  1;
        for(int i = 3; i <= n; i++){

            for(int j = 1; j < i - 1; j++){ //i-j > 1
            
            /*   
        		======= optimize: ========
             	for(int j = 1; j <= i / 2; j++) {
             	因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。 m>=2 so j <= i/2
        	*/
            
                dp[i] = Math.max(dp[i], Math.max(dp[i-j]*j,j*(i-j)));
            }
        }

        return dp[n];
    }
}

this is important :

dp[i] = Math.max(dp[i], Math.max(dp[i-j]j, j*(i-j) ));

dp[i-j]*j -> 至少是三个integer相乘

j*(i-j) -> 两个integer相乘

optimize : 因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话也是拆成m个近似数组的子数相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是最差也应该是拆成两个相同的可能是最大值。

那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。 j <=i/2

96. Unique Binary Search Trees

Given an integer n, return *the number of structurally unique **BST’*s (binary search trees) which has exactly n nodes of unique values from 1 to n.

Example 1:

1 2	Input: n = 3 Output: 5

class Solution {
    public int numTrees(int n) {
        if(n < 3){
            return n;
        }
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2 ; i < dp.length; i++){
            for(int j = 0; j < i; j++){
             //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j] * dp[i-j-1];
            }
        }
        return dp[n];
    }
}

https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0096.%E4%B8%8D%E5%90%8C%E7%9A%84%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.md

dp[0] = 1;

dp[1] =1,

dp[2] = 2;

dp[3] = dp[0] ( Case -> left tree has 0 node) * dp[2] (right tree has two nodes)+ dp[1] * dp[1] + dp[2] * dp[0]

不要忘记是需要累加的！

0/1 Knapsack problem:

装满背包的最大价值是多少
能不能装满一个背包
多少种方式能把背包装满

0/1 Knapsack Problem ( two dimenstion array)

确定递推公式:

dp [i] [j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

代码初始化如下：

for (int j = 0 ; j < weight[0]; j++) {  // 当然这一步，如果把dp数组预先初始化为0了，这一步就可以省略，但很多同学应该没有想清楚这一点。
    dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
}

public class BagProblem {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }


    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods][bagSize + 1];

        // 初始化dp数组
        // 创建数组后，其中默认的值就是0
        for (int j = weight[0]; j <= bagSize; j++) {
            dp[0][j] = value[0];
        }

        // 填充dp数组  两层for循环是可以颠倒的
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i-1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }

        // 打印dp数组
        for (int i = 0; i < goods; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}

动态规划-背包问题5

because dp[i ] [j] is caculated from dp [i- 1 ] [ j ],dp[i-1 ] [j-1 ], so 两层for循环是可以颠倒的

0/1 Knapsack Problem ( one dimenstion array)

确定dp数组的定义

在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。

一维dp数组的递推公式

dp[j]为容量为j的背包所背的最大价值，那么如何推导dp[j]呢？

dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j - weight[i]] + value[i] 表示容量为 j - 物品i重量的背包加上物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]）

此时dp[j]有两个选择，一个是取自己dp[j] 相当于二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值，

所以递归公式为：

1	dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

可以看出相对于二维dp数组的写法，就是把dp[i][j]中i的维度去掉了。

一维dp数组如何初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？

看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。

这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

那么我假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。

一维dp数组遍历顺序

代码如下：

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

************ one dimension: ********* 
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}
 ********* two  dimention: *********
 for (int i = 1; i < weight.length; i++) {
 	for (int j = 1; j <= bagSize; j++) {
		 if (j < weight[i]) {
 			dp[i][j] = dp[i-1][j];
 		} else {
 			dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
 		}
 	}
 }

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！！！！！！！！！！！！！！！！！！！！！

举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

为什么倒序遍历，就可以保证物品只放入一次呢？

倒序就是先算dp[2]

dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

dp[1] = dp[1 - weight[0]] + value[0] = 15

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

那么问题又来了，为什么二维dp数组历的时候不用倒序呢？

因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！所以倒叙正序都可以。

（如何这里读不懂，大家就要动手试一试了，空想还是不靠谱的，实践出真知！）

再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？

不可以！

因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

倒序遍历的原因是，本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。

（这里如果读不懂，就再回想一下dp[j]的定义，或者就把两个for循环顺序颠倒一下试试！）

所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的！，这一点大家一定要注意。

public static void main(String[] args) {
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWight = 4;
    testWeightBagProblem(weight, value, bagWight);
}

public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
    int wLen = weight.length;
    //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
    int[] dp = new int[bagWeight + 1];
    //遍历顺序：先遍历物品，再遍历背包容量
    for (int i = 0; i < wLen; i++){
        for (int j = bagWeight; j >= weight[i]; j--){
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    //打印dp数组
    for (int j = 0; j <= bagWeight; j++){
        System.out.print(dp[j] + " ");
    }
}

416. Partition Equal Subset Sum

Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.

Example 1:

1
2
3

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

my version(one dimension array):

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for(int i = 0; i < nums.length; i++){
            sum += nums[i];
        }
        if(sum % 2 != 0) return false;
        int half = sum/2;
        int[] dp = new int[half+1]; // notice here is half+1 not half
        for(int i = 0 ; i < nums.length; i++ ){
            for(int j = half; j >= nums[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }

        if(dp[half] == half){
            return true;
        }else{
            return false;
        }
    }
}

二维数组版本（易于理解）leetmaster：

public class Solution {
    public static void main(String[] args) {
        int num[] = {1,5,11,5};
        canPartition(num);

    }
    public static boolean canPartition(int[] nums) {
        int len = nums.length;
        // 题目已经说非空数组，可以不做非空判断
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // 特判：如果是奇数，就不符合要求
        if ((sum %2 ) != 0) {
            return false;
        }

        int target = sum / 2; //目标背包容量
        // 创建二维状态数组，行：物品索引，列：容量（包括 0）
        /*
        dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数
          每个数只能用一次，使得这些数的和恰好等于 j。
        */
        boolean[][] dp = new boolean[len][target + 1];

        // 先填表格第 0 行，第 1 个数只能让容积为它自己的背包恰好装满  （这里的dp[][]数组的含义就是“恰好”，所以就算容积比它大的也不要）
        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }
        // 再填表格后面几行
        //外层遍历物品
        for (int i = 1; i < len; i++) {
            //内层遍历背包
            for (int j = 0; j <= target; j++) {
                // 直接从上一行先把结果抄下来，然后再修正
                dp[i][j] = dp[i - 1][j];

                //如果某个物品单独的重量恰好就等于背包的重量，那么也是满足dp数组的定义的
                if (nums[i] == j) {
                    dp[i][j] = true;
                    continue;
                }
                //如果某个物品的重量小于j，那就可以看该物品是否放入背包
                //dp[i - 1][j]表示该物品不放入背包，如果在 [0, i - 1] 这个子区间内已经有一部分元素，使得它们的和为 j ，那么 dp[i][j] = true；
                //dp[i - 1][j - nums[i]]表示该物品放入背包。如果在 [0, i - 1] 这个子区间内就得找到一部分元素，使得它们的和为 j - nums[i]。
                if (nums[i] < j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
        }
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= target; j++) {
                System.out.print(dp[i][j]+" ");
            }
            System.out.println();
        }
        return dp[len - 1][target];
    }
}
//dp数组的打印结果
false true false false false false false false false false false false 
false true false false false true true false false false false false 
false true false false false true true false false false false true 
false true false false false true true false false false true true

my try:

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0 ; 
        for(int num : nums){
            sum += num;
        }
        if(sum % 2 != 0) return false;
        int[][] dp = new int[nums.length][sum/2 + 1];
        for( int j = nums[0]; j < sum/2; j++){
            dp[0][j] = nums[0];
        }

        for(int i = 1; i < nums.length; i++){
            for(int j = 1 ; j <= sum/2; j++){
                if(j < nums[i]) dp[i][j] = dp[i-1][j];
                else{
                    dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][j - nums[i]] + nums[i]);
                    if(dp[i][j] == sum/2) return true;
                }
            }
        }
        return false;
        
    }
}

1049. Last Stone Weight II

You are given an array of integers stones where stones[i] is the weight of the ith stone.

We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

If x == y, both stones are destroyed, and
If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.

At the end of the game, there is at most one stone left.

Return the smallest possible weight of the left stone. If there are no stones left, return 0.

Example 1:

Input: stones = [2,7,4,1,8,1]
Output: 1
Explanation:
We can combine 2 and 4 to get 2, so the array converts to [2,7,1,8,1] then,
we can combine 7 and 8 to get 1, so the array converts to [2,1,1,1] then,
we can combine 2 and 1 to get 1, so the array converts to [1,1,1] then,
we can combine 1 and 1 to get 0, so the array converts to [1], then that's the optimal value.

Example 2:

1 2	Input: stones = [31,26,33,21,40] Output: 5

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int i = 0; i < stones.length; i++){
            sum += stones[i];
        }
        int half = sum/2;
        int[] dp = new int[half+1];
        for(int i = 0; i < stones.length; i++){
            for(int j = half; j >= stones[i]; j--){
                dp[j] = Math.max(dp[j - stones[i]]+stones[i],dp[j]);
            }
        }

        int part1 = dp[half] ;
        int part2 =  sum - dp[half];
        return Math.abs(part1 - part2);

    }
}

494. Target Sum

纯 0 - 1 背包是求给定背包容量装满背包的最大价值是多少。
416. 分割等和子集是求给定背包容量，能不能装满这个背包。
1049. 最后一块石头的重量 II 是求给定背包容量，尽可能装，最多能装多少
494. 目标和是求给定背包容量，装满背包有多少种方法。
本题是求给定背包容量，装满背包最多有多少个物品。

You are given an integer array nums and an integer target.

You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".

Return the number of different expressions that you can build, which evaluates to target.

Example 1:

Input: nums = [1,1,1,1,1], target = 3
Output: 5
Explanation: There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

dp[j] ：装满容量为j的背包有dp[j]种方法

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来。

含义：dp【i】【j】：从下标为【0…i】的物品里任取，填满j这么⼤容积的包，有dp【i】【j】种⽅法
递推式：dp【i】【j】 = dp【i-1】【j】 + dp【i-1】[j-nums【i】]
dp【i-1】【j】是不将物品i放入背包的方式数，dp【i-1】[j-nums【i】]是将物品i放入背包的方式数
初始化：dp【0】【0】 = 1 表示装满容量为0的背包，有1种⽅法，就是装0件物品。（区别于原始的背包问题，它求的是最大价值，所以dp[0 】[0]=0因为没有东西所以总价值是0）
如果nums【0】在范围内的话，dp【0】[nums【0】] = 1
其他全为0

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) sum += nums[i];

        //如果target的绝对值大于sum，那么是没有方案的
        if (Math.abs(target) > sum) return 0;
        //如果(target+sum)除以2的余数不为0，也是没有方案的
        if ((target + sum) % 2 == 1) return 0;

        int bagSize = (target + sum) / 2;
        int[] dp = new int[bagSize + 1];
        dp[0] = 1;

        for (int i = 0; i < nums.length; i++) {
            for (int j = bagSize; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }

        return dp[bagSize];
    }
}

///////////////////////////////////////////////////////////////////

class Solution {
    public int findTargetSumWays(int[] nums, int target){       
        int sum = 0;
        for(int i=0; i < nums.length; i++){
            sum += nums[i];
        }
        if((target + sum)%2 != 0){
            return 0;
        }
        if(sum < Math.abs(target)){
            return 0;
        }

        int plus = (target + sum)/2;

        int[][] dp = new int[plus + 1][nums.length];

        for(int j = 0; j <= plus; j++) {
            if(nums[0] == j) {
                dp[j][0] = 1;
            }
        }

        int numZeros = 0;
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] == 0) {
                numZeros++;
            }
            dp[0][i] = (int) Math.pow(2, numZeros);

        }


         for(int i = 1; i < nums.length; i++){
             for(int j = 1; j <= plus; j++){
                if(nums[i] <= j){
                 dp[j][i] = dp[j - nums[i]][i-1] + dp[j][i-1];}else{
                dp[j][i] = dp[j][i-1];
                 }
             }
         }

         return dp[plus][nums.length-1];
    }
}

这道题感觉没讲清楚呀。。建议不懂的同学自己先用二维数组来做，比较好理解，理解了之后再用一维数组。
\1. 含义：dp【i】【j】：从下标为【0…i】的物品里任取，填满j这么⼤容积的包，有dp【i】【j】种⽅法
\2. 递推式：dp【i】【j】 = dp【i-1】【j】 + dp【i-1】[j-nums【i】]
dp【i-1】【j】是不将物品i放入背包的方式数，dp【i-1】[j-nums【i】]是将物品i放入背包的方式数
\3. 初始化：dp【0】【0】 = 1 表示装满容量为0的背包，有1种⽅法，就是装0件物品。
如果nums【0】在范围内的话，dp【0】[nums【0】] = 1
其他全为0
\4. 计算顺序：顺序，行优先

474. Ones and Zeroes

Medium

Companies

You are given an array of binary strings strs and two integers m and n.

Return the size of the largest subset of strs such that there are at most m 0‘s and n 1‘s in the subset.

A set x is a subset of a set y if all elements of x are also elements of y.

Example 1:

Input: strs = ["10","0001","111001","1","0"], m = 5, n = 3
Output: 4
Explanation: The largest subset with at most 5 0's and 3 1's is {"10", "0001", "1", "0"}, so the answer is 4.
Other valid but smaller subsets include {"0001", "1"} and {"10", "1", "0"}.
{"111001"} is an invalid subset because it contains 4 1's, greater than the maximum of 3.

Example 2:

1
2
3

Input: strs = ["10","0","1"], m = 1, n = 1
Output: 2
Explanation: The largest subset is {"0", "1"}, so the answer is 2.

// it's actually one dimmension solution
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        
        int[][] dp= new int[m+1][n+1]; // notice here, [m+1][n+1]
        dp[0][0] = 0;

        for( String str: strs){
            int one = 0;
            int zero = 0;
            for(char ch: str.toCharArray()){
                if(ch == '0') zero++;
                if(ch == '1') one++;
            }
            for(int i = m; i >= zero; i--){
                for(int j = n; j >= one; j--){
                    dp[i][j] = Math.max(dp[i][j],dp[i-zero][j-one]+1);
                }
            }
        }
        return dp[m][n];

    }
}

unbounded knapsack problem

遍历顺序从小到大就可以无限次选同一个物品

//先遍历物品，再遍历背包
private static void testCompletePack(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 0; i < weight.length; i++){ // 遍历物品
        for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

//先遍历背包，再遍历物品
private static void testCompletePackAnotherWay(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
        for (int j = 0; j < weight.length; j++){ // 遍历物品
            if (i - weight[j] >= 0){
                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
            }
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

518. Coin Change II

dp数组如何初始化

首先dp[0]一定要为1，dp[0] = 1是递归公式的基础。如果dp[0] = 0 的话，后面所有推导出来的值都是0了。

那么 dp[0] = 1 有没有含义，其实既可以说凑成总金额0的货币组合数为1，也可以说凑成总金额0的货币组合数为0，好像都没有毛病。

但题目描述中，也没明确说 amount = 0 的情况，结果应该是多少。

这里我认为题目描述还是要说明一下，因为后台测试数据是默认，amount = 0 的情况，组合数为1的。

下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]

dp[0]=1还说明了一种情况：如果正好选了coins[i]后，也就是j-coins[i] == 0的情况表示这个硬币刚好能选，此时dp[0]为1表示只选coins[i]存在这样的一种选法。

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount+1];
        dp[0] =1;
        for(int i = 0; i < coins.length; i++){
            for(int j = coins[i]; j <= amount; j++){
                dp[j] = dp[j]+dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

377. Combination Sum IV

Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

The test cases are generated so that the answer can fit in a 32-bit integer.

Example 1:

Input: nums = [1,2,3], target = 4
Output: 7
Explanation:
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

logic one: 就是说先遍历物品的时候相当于是先把这个物品放进去了然后再看其他的能不能放进去，所以不会出现逆序，先遍历背包相当于是用每个大小的背包看看把每一个物品都放进去一次再看别的物品能不能放进去，所以可以有逆序

logic 2: 关于组合和排列的问题还是有些不解。以下仅为自己的理解：先遍历物品后遍历背包是这样，比如，外层循环固定coins【1】，在内层循环遍历背包时，随着背包不断增加，coins【1】可以重复被添加进来，而由于外层循环固定了，因此coins【2】只能在下一次外层循环添加进不同大小的背包中，这么看的话，coins【i+1】只能在coins【i】之后了；如果先遍历背包后遍历物品，那么外层循环先固定背包大小j，然后在大小为j的背包中循环遍历添加物品，然后在下次外层循环背包大小变为j+1，此时仍要执行内层循环遍历添加物品，也就会出现在上一轮外层循环中添加coins【2】的基础上还能再添加coins【1】的情况，那么就有了coins【1】在coins【2】之后的情况了。

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for(int j = 0; j <= target; j++)
        {
            for(int i = 0; i < nums.length; i++)
            {
                if(nums[i] <= j){
                    dp[j] = dp[j] + dp[j-nums[i]];
                }
            }
        }

        return dp[target];
    }
}

322. Coin Change

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

1
2
3

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

The check if(dp[j-coins[i]]!= Integer.MAX_VALUE) is necessary to ensure that we only consider valid subproblem solutions. If dp[j - coins[i]] is equal to Integer.MAX_VALUE, it means that there is no valid solution for the amount j - coins[i], and hence, we cannot use the current coin denomination to make up the amount j.

Without this check, the algorithm might end up considering invalid solutions and could produce incorrect results. This check ensures that we only consider valid intermediate solutions to compute the fewest number of coins for the given amount.

class Solution {
    public int coinChange(int[] coins, int amount){ 

        int[] dp = new int[amount + 1];
        for(int j = 0; j <= amount; j++){
            dp[j] = Integer.MAX_VALUE; //important!
        }
        dp[0] = 0;//题目里面就可以看出
        for(int i =0; i < coins.length; i++){//这道题用排列/组合都是可以的
            for(int j = coins[i]; j < amount+1; j++){
                if(dp[j-coins[i]]!= Integer.MAX_VALUE) //important!!
                //只有dp[j-coins[i]]不是初始最大值时，该位才有选择的必要
                dp[j] = Math.min(dp[j], dp[j-coins[i]]+1);
                //cant be:  dp[j] = dp[j - coins[i]] + 1;
            }
        }
        if(dp[amount]<0 || dp[amount] == Integer.MAX_VALUE){
            return -1;
        }
        return dp[amount];
    }
}

139.Word Break

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example :

1
2
3

Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

确定遍历顺序

题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。

还要讨论两层for循环的前后顺序。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

我在这里做一个总结：

而本题其实我们求的是排列数，为什么呢。拿 s = “applepenapple”, wordDict = [“apple”, “pen”] 举例。

“apple”, “pen” 是物品，那么我们要求物品的组合一定是 “apple” + “pen” + “apple” 才能组成 “applepenapple”。

“apple” + “apple” + “pen” 或者 “pen” + “apple” + “apple” 是不可以f的，那么我们就是强调物品之间顺序。

所以说，本题一定是先遍历背包，再遍历物品。

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        HashSet<String> set = new HashSet<>(wordDict);
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;
        for(int j = 1; j < dp.length; j++ ){
            for(int i = 0 ; i < j; i++){
                if(dp[i] == true && dp[j] == false && set.contains(s.substring(i,j)) ){
                    dp[j] = true;
                }
            }
           
        }
         return dp[s.length()];
    }
}

198. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1)  return nums[0];

        int[] dp = new int[nums.length];
        dp[0] = nums[0];//!!!!
        dp[1] = Math.max(nums[0], nums[1]);  //important
        
        for(int i = 2; i < nums.length; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2]+ nums[i]); //important
        }

        return dp[nums.length - 1];
    }
}

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

213. House Robber II

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

1
2
3

Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.

这道题目和198.打家劫舍是差不多的，唯一区别就是成环了。

对于一个数组，成环的话主要有如下三种情况：

情况一：考虑不包含首尾元素
情况二：考虑包含首元素，不包含尾元素

情况三：考虑包含尾元素，不包含首元素

**注意我这里用的是”考虑”**，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！对于情况三，取nums[1] 和 nums[3]就是最大的。

而情况二和情况三都包含了情况一了，所以只考虑情况二和情况三就可以了。

分析到这里，本题其实比较简单了。剩下的和198.打家劫舍就是一样的了。

class Solution {
    public int robRange(int[] nums, int start, int end){
        int[] dp = new int[end - start + 1];
        dp[0] = nums[start];
        dp[1] = Math.max(nums[start] , nums[start+1]);
        for(int i = 2; i <= end - start ; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i+start]);
        }

        return dp[end - start];
    }

    public int rob(int[] nums) {
        if(nums.length == 1) return nums[0];
        if(nums.length == 2) return Math.max(nums[0] , nums[1]);
        int a = robRange(nums, 1 , nums.length - 1);
        int b = robRange(nums, 0 , nums.length - 2);

        return Math.max(a, b);
    }
}

//wrong version: its very hard to imitate the process in my mind
class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1) return nums[0];
        return Math.max(count(0, nums.length - 2,nums), count(1, nums.length - 1,nums));
    }
    public int count(int start, int end, int[] nums){
        int[] dp = new int[end - start + 1];
        dp[0] = nums[start];
        dp[1] = Math.max(dp[0], nums[start + 1]);
        for(int i = 2 ; i <= end; i++){
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[start + i]);
        }
        return dp[end - start];
    }
}

337. House Robber III

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example 1:

1
2
3

Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

//1. time out
class Solution {
    public int rob(TreeNode root) {
        int[] res = robb(root);
        return Math.max(res[0], res[1]);
    }
    public int[] robb(TreeNode node){
        
        int[] res = new int[2];
        if(node == null) return res;

        // no rob
        res[0] = Math.max(robb(node.left)[0],robb(node.left)[1]) + Math.max(robb(node.right)[0],robb(node.right)[1]);
        // rob
        res[1] = node.val + robb(node.left)[0] + robb(node.right)[0];
        return res;
    }
}


//2:  correct
class Solution {
    public int rob(TreeNode root) {
        int[] res = robb(root);
        return Math.max(res[0], res[1]);
    }
    public int[] robb(TreeNode node){
        
        int[] res = new int[2];
        if(node == null) return res;
        int[] left = robb(node.left);
        int[] right = robb(node.right);
        // no rob
        res[0] = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);
        // rob
        res[1] = node.val + left[0] + right[0];
        return res;
    }
}

121. Best Time to Buy and Sell Stock

Easy

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:

1
2
3

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

class Solution {
    public int maxProfit(int[] prices) {
        if ( prices.length == 0) return 0;
        int[][] dp= new int[prices.length][2];
        dp[0][0] = 0; // not holding any stock ()
        dp[0][1] = -prices[0];   //hold some stock
        for(int i = 1 ; i < prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i-1][1],  - prices[i]);
            //dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); if you write this way, then it means that you can buy and sell more than once!!!!!!!!!!!!!!
        }
        return dp[prices.length - 1][0]; 
    }
}

122. Best Time to Buy and Sell Stock II

Medium

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.

On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.

Find and return the maximum profit you can achieve.

本题和121. 买卖股票的最佳时机的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）

在动规五部曲中，这个区别主要是体现在递推公式上，其他都和121. 买卖股票的最佳时机一样一样的。

本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。

那么第i天持有股票即dp[i][0]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i - 1] [1] - prices[i]。

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.

Example 3:

1
2
3

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 ) return 0;
        int[][] dp = new int[prices.length][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1 ; i < prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }
        return dp[prices.length - 1][0];
    }
}

123. Best Time to Buy and Sell Stock III

Hard

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete at most two transactions.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:


Input: prices = [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

//还是要把dp[i][0]当成没有任何操作， 如果把dp[i][0]当成第一次不持有的话，其实很容易搞混，因为它有可能是已经卖出去一次了，或者是说一次都没有买过。
//这里最好用dp[len][5]啦
class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 ) return 0;
        int[][] dp = new int[prices.length][4];
        dp[0][0] = 0; //理解成同一天买入同一天卖出！！！！！！ //first time not to have
        dp[0][1] = -prices[0]; //first time to have
        dp[0][2] = 0; // second time not to have
        dp[0][3] = -prices[0]; // second time to have
        for(int i = 1 ; i < prices.length; i++){
            
            // first time to hold a stock
            dp[i][1] = Math.max(dp[i-1][1], 0 - prices[i]);
            // first time not to hold any stock
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]); 
            
            // second time to hold a stock
            dp[i][3] = Math.max(dp[i-1][3], dp[i-1][0] - prices[i]);
            // second time not to hold any stock
            dp[i][2] = Math.max(dp[i-1][2], dp[i-1][3] + prices[i]);
        }
        return Math.max(dp[prices.length - 1][0],dp[prices.length - 1][2]);
    }
}

188. Best Time to Buy and Sell Stock IV

Hard

You are given an integer array prices where prices[i] is the price of a given stock on the ith day, and an integer k.

Find the maximum profit you can achieve. You may complete at most k transactions: i.e. you may buy at most k times and sell at most k times.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

1
2
3

Input: k = 2, prices = [2,4,1]
Output: 2
Explanation: Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.

Example 2:

1
2
3

Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

//wrong
//还是要把dp[i][0]当成没有任何操作， 如果把dp[i][0]当成第一次不持有的话，其实很容易搞混，因为它有可能是已经卖出去一次了，或者是说一次都没有买过。
class Solution {
    public int maxProfit(int k, int[] prices) {
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2*k];///////////////////////
        for(int i = 0 ; i < k*2; i++){
            if(i % 2 == 0){
                dp[0][i] = 0;
            }else{
                dp[0][i] = -prices[0];
            }
        }
        //////////////////////////////////////////////////////
        for(int i = 1 ; i < prices.length; i++){
            for(int j = 0 ; j < k*2 ; j++){
                if(j%2 == 0){
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j + 1] + prices[i]);
                }else{
                     dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - 1] - prices[i]);

                }
            }
        }
        return dp[prices.length - 1][k];
        /////////////////////////////////////////////////////////
    }
}
//right:
class Solution {
    public int maxProfit(int k, int[] prices) {
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2*k + 1];
        for(int i = 0 ; i < k*2; i++){
            if(i % 2 == 0){
                dp[0][i] = 0;
            }else{
                dp[0][i] = -prices[0];
            }
        }
         for (int i = 1; i < prices.length; i++) {
            for (int j = 0; j < k*2 - 1; j += 2) {
                dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.length - 1][k*2];
    }
}
//modified:
class Solution {
    public int maxProfit(int k, int[] prices) {
        if(prices.length == 0) return 0;
        int[][] dp = new int[prices.length][2*k + 1];///////////////////////
        for(int i = 0 ; i < k*2 + 1; i++){
            if(i % 2 == 0){
                dp[0][i] = 0;
            }else{
                dp[0][i] = -prices[0];
            }
        }
        //////////////////////////////////////////////////////
        for(int i = 1 ; i < prices.length; i++){
            for(int j = 1 ; j < k*2 + 1 ; j++){
                if(j%2 == 0){
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - 1] + prices[i]);
                }else{
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - 1] - prices[i]);
                }
            }
        }
        return dp[prices.length - 1][2*k];
        /////////////////////////////////////////////////////////
    }
}

309. Best Time to Buy and Sell Stock with Cooldown

Medium

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:

After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

1
2
3

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int k = prices.length;
        int[][] dp = new int[prices.length][4];
        ///////////////////////////////////////////////////////
        dp[0][0] = -prices[0];
        //////////////////////////////////////////////////////
        for(int i = 1 ; i < prices.length; i++){
            for(int j = 1 ; j < 4 ; j++){
                dp[i][0] = Math.max(Math.max(dp[i-1][0], dp[i-1][3] - prices[i]), dp[i-1][1] - prices[i]);
                dp[i][1] = Math.max(dp[i-1][1], dp[i-1][3]);
                dp[i][2] = dp[i-1][0] +prices[i];
                dp[i][3] = dp[i-1][2];
            }
        }
        return Math.max(Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2] ),dp[prices.length - 1][3]);
        /////////////////////////////////////////////////////////
    }
}

300. Longest Increasing Subsequence

Medium

Given an integer array nums, return the length of the longest strictly increasing subsequence

Example 1:

1
2
3

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int res = 1;
        for(int i = 1 ; i < nums.length; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[j] + 1, dp[i]);
                }
                res = Math.max(res, dp[i]); //!!!
            }
        }
        return res;//!!!! 注意这里不是返回nums[len-1];
    }
}

dp[]这个数组最后，不是递增的。比如说nums[2,3,1,5,4]

for the array nums = [2,3,1,5,4], the dp array would be [1, 2, 1, 3, 3].

好不懂的话自己举例自己手算dp数组

674. Longest Continuous Increasing Subsequence easy version of 300

Easy

Given an unsorted array of integers nums, return the length of the longest continuous increasing subsequence (i.e. subarray). The subsequence must be strictly increasing.

A continuous increasing subsequence is defined by two indices l and r (l < r) such that it is [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] and for each l <= i < r, nums[i] < nums[i + 1].

Example 1:

Input: nums = [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5] with length 3.
Even though [1,3,5,7] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element
4.

Example 2:

Input: nums = [2,2,2,2,2]
Output: 1
Explanation: The longest continuous increasing subsequence is [2] with length 1. Note that it must be strictly
increasing.

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp,1);
        int res = 1;
        for(int i = 1 ; i < nums.length; i++){
            if(nums[i] > nums[i-1])
                dp[i] =  dp[i-1] + 1;
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

概括来说：不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关

贪心法：

public static int findLengthOfLCIS(int[] nums) {
    if (nums.length == 0) return 0;
    int res = 1; // 连续子序列最少也是1
    int count = 1;
    for (int i = 0; i < nums.length - 1; i++) {
        if (nums[i + 1] > nums[i]) { // 连续记录
            count++;
        } else { // 不连续，count从头开始
            count = 1;
        }
        if (count > res) res = count;
    }
    return res;
}

718. Maximum Length of Repeated Subarray

Medium

Given two integer arrays nums1 and nums2, return the maximum length of a subarray that appears in both arrays.

Example 1:

1
2
3

Input: nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
Output: 3
Explanation: The repeated subarray with maximum length is [3,2,1].

Example 2:

1
2
3

Input: nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
Output: 5
Explanation: The repeated subarray with maximum length is [0,0,0,0,0].

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];
        int res = 0;
        for(int i = 0 ; i < nums1.length ; i++){
            for(int j = 0 ; j < nums2.length ; j++){
                if(nums1[i] == nums2[j]){
                    dp[i + 1 ][j + 1] = dp[i][j] + 1;
                }
                res = Math.max(res, dp[i+1][j+1]);
            }
        }
        return res; 
    }
}

https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0718.%E6%9C%80%E9%95%BF%E9%87%8D%E5%A4%8D%E5%AD%90%E6%95%B0%E7%BB%84.md

1143. Longest Common Subsequence

Medium

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

1
2
3

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

1
2
3

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];

        for(int i = 0 ; i < text1.length() ; i++){
            for(int j = 0; j < text2.length() ; j++){
                if(text1.charAt(i) == text2.charAt(j)){
                    dp[i+1][j+1] = dp[i][j] + 1;
                    // j++;
                    // while(j+1 < text2.length() + 1){
                    //     dp[i+1][j+1] =dp[i+1][j];
                    //     System.out.println(dp[i+1][j+1]);
                    //     j++;
                       
                    // }
                }else{
                    dp[i+1][j+1] = Math.max(dp[i][j+1], dp[i+1][j]);
                }
            }
        }
        
        return dp[text1.length()][text2.length()];
    }
}

确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码如下：

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

1035. Uncrossed Lines

这道题难点是剥开外壳，其实就是让你求最长子序列跟上一道题一样

Medium

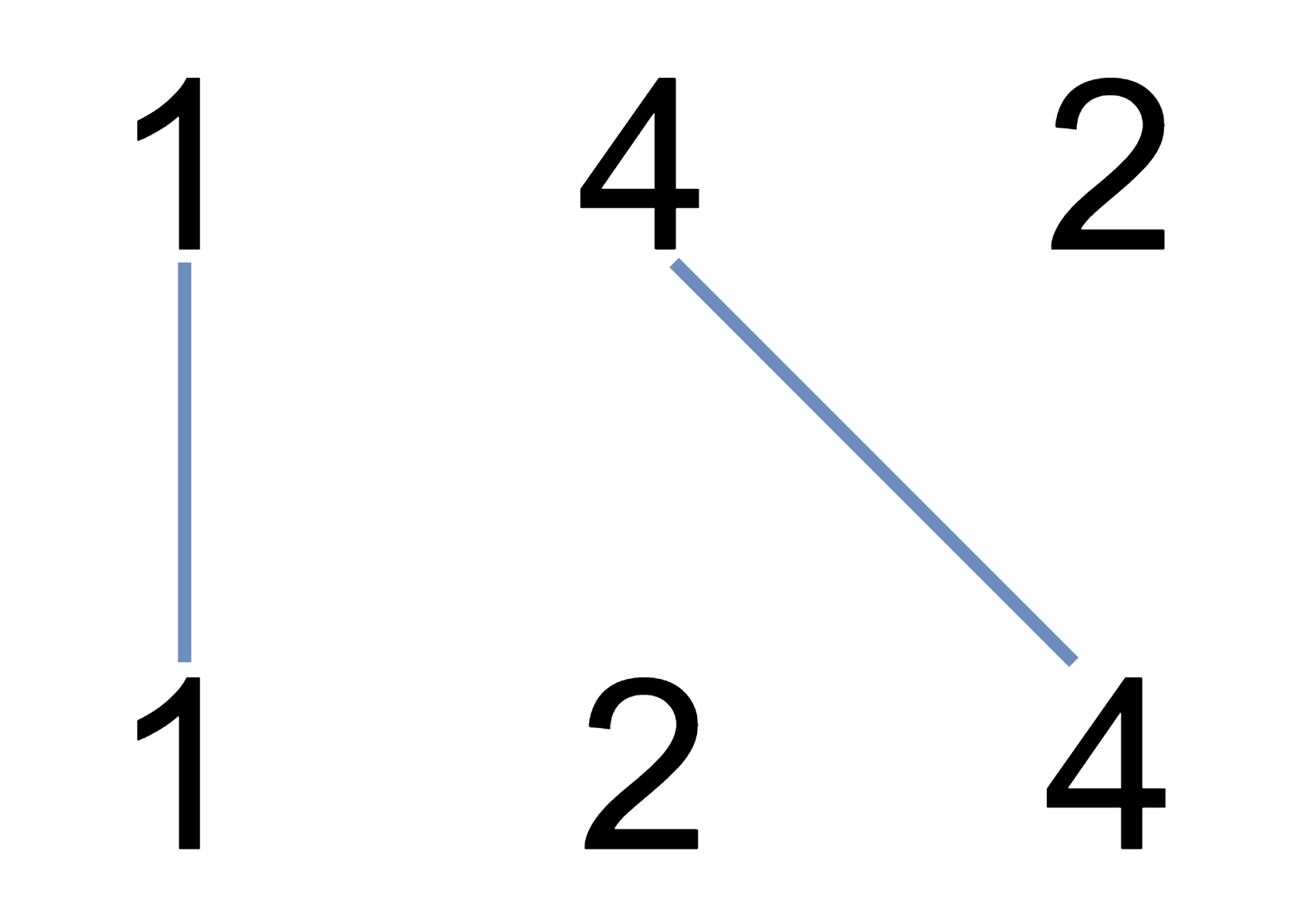
You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1:

Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
         int[][] dp = new int[nums1.length + 1][nums2.length + 1];

        for(int i = 0 ; i < nums1.length ; i++){
            for(int j = 0; j < nums2.length ; j++){
                if(nums1[i] ==nums2[j]){
                    dp[i+1][j+1] = dp[i][j] + 1;
                    // j++;
                    // while(j+1 < text2.length() + 1){
                    //     dp[i+1][j+1] =dp[i+1][j];
                    //     System.out.println(dp[i+1][j+1]);
                    //     j++;
                       
                    // }
                }else{
                    dp[i+1][j+1] = Math.max(dp[i][j+1], dp[i+1][j]);
                }
            }
        }
        
        return dp[nums1.length][nums2.length];
    }
}

392. Is Subsequence

Easy

Given two strings s and t, return true if s is a subsequence of t, or false otherwise.

A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).

Example 1:

1 2	Input: s = "abc", t = "ahbgdc" Output: true

Example 2:

1 2	Input: s = "axc", t = "ahbgdc" Output: false

class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][] dp = new int[s.length()+1][t.length()+1];
        for(int i = 1 ; i < s.length()+1; i++){
            for(int j = 1 ; j < t.length()+1; j++){
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[s.length()][t.length()]==s.length();
    }
}

115. Distinct Subsequences

Hard

Given two strings s and t, return the number of distinct *subsequences* of s which equals t.

The test cases are generated so that the answer fits on a 32-bit signed integer.

Example 1:

Input: s = "rabbbit", t = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from s.
rabbbit
rabbbit
rabbbit

279. Perfect Squares

Given an integer n, return the least number of perfect square numbers that sum to n.

A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.

Example 1:

1
2
3

Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.

Example 2:

1
2
3

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for(int i = 0; i < dp.length; i++){
            dp[i] = Integer.MAX_VALUE;
        }
        dp[0] = 0;
        for(int j = 1; j <= n; j++){
            for(int i = 1 ; i <= n; i++){
                if(i*i <= j)
                dp[j] = Math.min(dp[j - i*i] + 1, dp[j]);
            }
        }
        return dp[n];
    }
}

115. Distinct Subsequences

Hard

Given two strings s and t, return the number of distinct *subsequences* of s which equals t.

The test cases are generated so that the answer fits on a 32-bit signed integer.

Example 1:

Input: s = "rabbbit", t = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from s.
rabbbit
rabbbit
rabbbit

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length()+1][t.length()+1];
    for (int i = 0; i <= s.length(); i++) dp[i][0] = 1;
    for (int j = 1; j <= t.length(); j++) dp[0][j] = 0;
        for(int i = 1; i < s.length()+1; i++){
            for(int j = 1; j < t.length()+1; j++){
                if(s.charAt(i-1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

为什么i-1，j-1 这么定义我在 718. 最长重复子数组中做了详细的讲解。

确定递推公式

这一类问题，基本是要分析两种情况

s[i - 1] 与 t[j - 1]相等
s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。

一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

这里可能有录友不明白了，为什么还要考虑不用s[i - 1]来匹配，都相同了指定要匹配啊。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

这里可能有录友还疑惑，为什么只考虑 “不用s[i - 1]来匹配” 这种情况，不考虑 “不用t[j - 1]来匹配” 的情况呢。

这里大家要明确，我们求的是 s 中有多少个 t，而不是求t中有多少个s，所以只考虑 s中删除元素的情况，即不用s[i - 1]来匹配的情况。

dp数组如何初始化

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。

每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

初始化分析完毕，代码如下：

1
2
3

vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起，但我为了凸显初始化的逻辑，所以还是加上了。

583. Delete Operation for Two Strings

Medium

Given two strings word1 and word2, return the minimum number of steps required to make word1 and word2 the same.

In one step, you can delete exactly one character in either string.

Example 1:

1
2
3

Input: word1 = "sea", word2 = "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".

Example 2:

1 2	Input: word1 = "leetcode", word2 = "etco" Output: 4

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length()+1][word2.length()+1];
        for(int i = 0 ;  i < word1.length(); i++) dp[i][0] = i;
         for(int i = 0 ;  i < word2.length(); i++) dp[0][i] = i;
        for(int i = 1; i < word1.length() +1; i++){
            for(int j = 1; j < word2.length()+1; j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(Math.min(dp[i-1][j-1] + 1, dp[i-1][j]+1),dp[i][j-1]+1); //!!!!!!
                }
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

确定递推公式

当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2，所以递推公式可简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);

这里可能不少录友有点迷糊，从字面上理解就是当同时删word1[i - 1]和word2[j - 1]，dp[i][j-1] 本来就不考虑 word2[j - 1]了，那么我在删 word1[i - 1]，是不是就达到两个元素都删除的效果，即 dp[i][j-1] + 1。

dp数组如何初始化

从递推公式中，可以看出来，dp[i][0] 和 dp[0][j]是一定要初始化的。

dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i。

dp[0][j]的话同理，所以代码如下：

1
2
3

vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;

72. Edit Distance

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

Insert a character
Delete a character
Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for(int i = 0 ; i < word1.length() + 1; i++){
            dp[i][0] = i;
        }
        for(int j = 0 ; j < word2.length() + 1; j++){
            dp[0][j] = j;
        }
        for(int i = 1 ; i < word1.length() + 1; i++){
            for(int j = 1 ; j < word2.length() + 1; j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(Math.min(dp[i-1][j] + 1, dp[i][j-1]+1), dp[i-1][j-1]+1);
                }
                    
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

确定dp数组（dp table）以及下标的含义

**dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]**。

有同学问了，为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？

为什么这么定义我在 718. 最长重复子数组中做了详细的讲解。

其实用i来表示也可以！用i-1就是为了方便后面dp数组初始化的。

确定递推公式

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
    不操作
if (word1[i - 1] != word2[j - 1])
    增
    删
    换

也就是如上4种情况。

1	if (word1[i - 1] == word2[j - 1])` 那么说明不用任何编辑，`dp[i][j]` 就应该是 `dp[i - 1][j - 1]`，即`dp[i][j] = dp[i - 1][j - 1];

此时可能有同学有点不明白，为啥要即dp[i][j] = dp[i - 1][j - 1]呢？

那么就在回顾上面讲过的dp[i][j]的定义，word1[i - 1] 与 word2[j - 1]相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。

在下面的讲解中，如果哪里看不懂，就回想一下dp[i][j]的定义，就明白了。

在整个动规的过程中，最为关键就是正确理解dp[i][j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离再加上一个操作。

即 dp[i][j] = dp[i - 1][j] + 1;

操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离再加上一个操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是删除元素，添加元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"，最终的操作数是一样！ dp数组如下图所示意的：

           a                         a     d
  +-----+-----+             +-----+-----+-----+
  |  0  |  1  |             |  0  |  1  |  2  |
  +-----+-----+   ===>      +-----+-----+-----+
a |  1  |  0  |           a |  1  |  0  |  1  |
  +-----+-----+             +-----+-----+-----+
d |  2  |  1  |
  +-----+-----+

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。

可以回顾一下，if (word1[i - 1] == word2[j - 1])的时候我们的操作是 dp[i][j] = dp[i - 1][j - 1] 对吧。

那么只需要一次替换的操作，就可以让 word1[i - 1] 和 word2[j - 1] 相同。

所以 dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

SUM UP: 编辑距离

https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E4%B8%BA%E4%BA%86%E7%BB%9D%E6%9D%80%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB%EF%BC%8C%E5%8D%A1%E5%B0%94%E5%81%9A%E4%BA%86%E4%B8%89%E6%AD%A5%E9%93%BA%E5%9E%AB.md

647. Palindromic Substrings

Medium

Given a string s, return the number of palindromic substrings in it.

A string is a palindrome when it reads the same backward as forward.

A substring is a contiguous sequence of characters within the string.

Example 1:

1
2
3

Input: s = "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".

class Solution {
    public int countSubstrings(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        for(int i = 0 ; i < s.length(); i++){
            for(int j = 0 ; j < s.length(); j++){
                dp[i][j] = false; //actually those are not necessary cause boolean is defaulted to be false
            }
        }
        int res = 0;
         for(int i = s.length() - 1 ; i >= 0; i--){ //!!!! decreasing order!!
            for(int j = i ; j < s.length(); j++){ // starting from i !!!
                if(s.charAt(i) == s.charAt(j))
                    if(i==j){
                        dp[i][j] = true;
                        res++;
                    }else if( j - i == 1){
                        dp[i][j] = true;
                        res++;
                    }else{
                        dp[i][j] = dp[i + 1][j-1]; //!!! noti-1 ,j-1
                        if(dp[i][j] == true) res++;
                    }
            }
         }
         return res;
    }
}

确定dp数组（dp table）以及下标的含义

如果大家做了很多这种子序列相关的题目，在定义dp数组的时候很自然就会想题目求什么，我们就如何定义dp数组。

绝大多数题目确实是这样，不过本题如果我们定义，dp[i] 为下标i结尾的字符串有 dp[i]个回文串的话，我们会发现很难找到递归关系。

dp[i] 和 dp[i-1] ，dp[i + 1] 看上去都没啥关系。

所以我们要看回文串的性质。如图：

我们在判断字符串S是否是回文，那么如果我们知道 s[1]，s[2]，s[3] 这个子串是回文的，那么只需要比较 s[0]和s[4]这两个元素是否相同，如果相同的话，这个字符串s 就是回文串。

那么此时我们是不是能找到一种递归关系，也就是判断一个子字符串（字符串的下表范围[i,j]）是否回文，依赖于，子字符串（下表范围[i + 1, j - 1]））是否是回文。

所以为了明确这种递归关系，我们的dp数组是要定义成一位二维dp数组。

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

确定递推公式

在确定递推公式时，就要分析如下几种情况。

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

以上三种情况分析完了，那么递归公式如下：

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

result就是统计回文子串的数量。

注意这里我没有列出当s[i]与s[j]不相等的时候，因为在下面dp[i][j]初始化的时候，就初始为false。

dp数组如何初始化

dp[i][j]可以初始化为true么？当然不行，怎能刚开始就全都匹配上了。

所以dp[i][j]初始化为false。

确定遍历顺序

遍历顺序可有有点讲究了。

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。

dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

如果这矩阵是从上到下，从左到右遍历，那么会用到没有计算过的dp[i + 1][j - 1]，也就是根据不确定是不是回文的区间[i+1,j-1]，来判断了[i,j]是不是回文，那结果一定是不对的。

所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

[toc]

DP🌼

Summarize:

What’s DP?

Dynamic Programming Five Steps:

1. Fundamental questions

climbing stairs

summary

3. “House Robber” series

4. stock problem

Sample question:

steps:

Leetcode:

62. Unique Paths

63.Unique Paths II

0/1 Knapsack problem:

0/1 Knapsack Problem ( two dimenstion array)

0/1 Knapsack Problem ( one dimenstion array)

一维dp数组如何初始化

474. Ones and Zeroes

unbounded knapsack problem

139.Word Break

674. Longest Continuous Increasing Subsequence easy version of 300

SUM UP: 编辑距离