Binary Tree

Types of binary tree

1. Full Binary Tree

A full Binary tree is a special type of binary tree in which every parent node/internal node has either two or no children.

Full binary tree

To learn more, please visit full binary tree.

2. Perfect Binary Tree

A perfect binary tree is a type of binary tree in which** every internal node has exactly two child nodes and all the leaf nodes are at the same level.**

Perfect binary treePerfect Binary Tree

To learn more, please visit perfect binary tree.

3. Complete Binary Tree

A complete binary tree is just like a full binary tree, but with two major differences

  1. Every level must be completely filled
  2. All the leaf elements must lean towards the left.
  3. The last leaf element might not have a right sibling i.e. a complete binary tree doesn’t have to be a full binary tree.

Complete Binary TreeComplete Binary Tree

To learn more, please visit complete binary tree.

4. Degenerate or Pathological Tree

A degenerate or pathological tree is the tree having a single child either left or right .

Degenerate Binary Tree

5. Skewed Binary Tree

A skewed binary tree is a pathological/degenerate tree in which the tree is either dominated by the left nodes or the right nodes. Thus, there are two types of skewed binary tree: left-skewed binary tree and right-skewed binary tree.

Skewed Binary TreeSkewed Binary Tree

6. Balanced Binary Tree

It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1.

Balanced Binary TreeBalanced Binary Tree

To learn more, please visit balanced binary tree.

Complete binary tree

Max heap / Min heap

Heap data structure is a complete binary tree that satisfies the heap property, where any given node is

  • always greater than its child node/s and the key of the root node is the largest among all other nodes. This property is also called max heap property.
  • always smaller than the child node/s and the key of the root node is the smallest among all other nodes. This property is also called min heap property.

Max-heapMax-heap↓

Min-heapMin-heap↓

This type of data structure is also called a binary heap.

Heap operation

Heapify

Heapify is the process of creating a heap data structure from a binary tree. It is used to create a Min-Heap or a Max-Heap.

  1. Let the input array be

    heap initial array

  2. Create a complete binary tree from the array

    Complete binary tree

  3. Start from the first index of non-leaf node whose index is given by n/2 - 1.

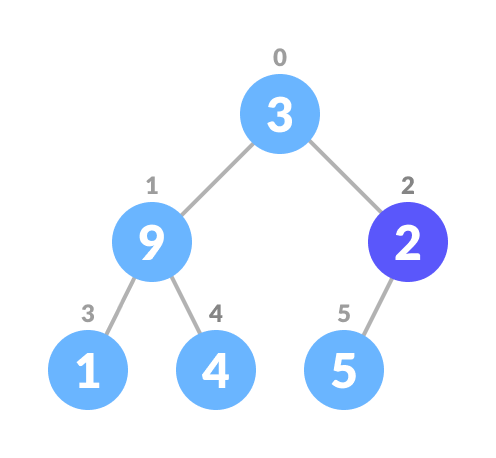
    heapify leaf node

  4. Set current element i as largest.

  5. The index of left child is given by 2i + 1 and the right child is given by 2i + 2.
    If leftChild is greater than currentElement (i.e. element at ith index), set leftChildIndex as largest.
    If rightChild is greater than element in largest, set rightChildIndex as largest.

  6. Swap largest with currentElement

    heapify

  7. Repeat steps 3-7 until the subtrees are also heapified.

Algorithm

1
2
3
4
5
6
7
8
9
10
11
Heapify(array, size, i)
  set i as largest
  leftChild = 2i + 1
  rightChild = 2i + 2
  
  if leftChild > array[largest]
    set leftChildIndex as largest
  if rightChild > array[largest]
    set rightChildIndex as largest

  swap array[i] and array[largest]

To create a Max-Heap:

1
2
3
MaxHeap(array, size)
  loop from the first index of non-leaf node down to zero
    call heapify

For Min-Heap, both leftChild and rightChild must be larger than the parent for all nodes.

Insert Element into Heap

Algorithm for insertion in Max Heap

1
2
3
4
5
6
If there is no node, 
  create a newNode.
else (a node is already present)
  insert the newNode at the end (last node from left to right.)
  
heapify the array

  1. Insert the new element at the end of the tree.

    insertion in heap

  2. Heapify the tree.

insertion in heap

For Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.

Delete Element from Heap

Algorithm for deletion in Max Heap

1
2
3
4
5
6
If nodeToBeDeleted is the leafNode
  remove the node
Else swap nodeToBeDeleted with the lastLeafNode
  remove noteToBeDeleted
   
heapify the array

  1. Select the element to be deleted.

    deletion in heap

  2. Swap it with the last element.

    deletion in heap

  3. Remove the last element.

    deletion in heap

  4. Heapify the tree.

deletion in heap

For Min Heap, above algorithm is modified so that both childNodes are greater smaller than currentNode.

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
// Max-Heap data structure in Java

import java.util.ArrayList;

class Heap {
  void heapify(ArrayList<Integer> hT, int i) {
    int size = hT.size();
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < size && hT.get(l) > hT.get(largest))
      largest = l;
    if (r < size && hT.get(r) > hT.get(largest))
      largest = r;

    if (largest != i) {
      int temp = hT.get(largest);
      hT.set(largest, hT.get(i));
      hT.set(i, temp);

      heapify(hT, largest);
    }
  }

  void insert(ArrayList<Integer> hT, int newNum) {
    int size = hT.size();
    if (size == 0) {
      hT.add(newNum);
    } else {
      hT.add(newNum);
      for (int i = size / 2 - 1; i >= 0; i--) {
        heapify(hT, i);
      }
    }
  }

  void deleteNode(ArrayList<Integer> hT, int num)
  {
    int size = hT.size();
    int i;
    for (i = 0; i < size; i++)
    {
      if (num == hT.get(i))
        break;
    }

    int temp = hT.get(i);
    hT.set(i, hT.get(size-1));
    hT.set(size-1, temp);

    hT.remove(size-1);
    for (int j = size / 2 - 1; j >= 0; j--)
    {
      heapify(hT, j);
    }
  }

  void printArray(ArrayList<Integer> array, int size) {
    for (Integer i : array) {
      System.out.print(i + " ");
    }
    System.out.println();
  }

  public static void main(String args[]) {

    ArrayList<Integer> array = new ArrayList<Integer>();
    int size = array.size();

    Heap h = new Heap();
    h.insert(array, 3);
    h.insert(array, 4);
    h.insert(array, 9);
    h.insert(array, 5);
    h.insert(array, 2);

    System.out.println("Max-Heap array: ");
    h.printArray(array, size);

    h.deleteNode(array, 4);
    System.out.println("After deleting an element: ");
    h.printArray(array, size);
  }
}

MaxHeapify VS. BuildMaxHeap

Basically, heapify is an algorithm used to re-arrange the heap if the root node violates the heap property (child subtrees must be heaps!). It’s a vital part of building a heap, inserting or deleting a top node from the heap.

Heapify is:

  • after we popped the top node of the heap and we moved the last node to the top then we rearrange the tree from top-to-bottom so it is a heap again (we heapify)
  • heapify time complexity O(log n)

Heapify is not:

creating a heap from an array which is a bottom-up operation with a time complexity of O(n)

even though heapify is actively used for building a heap, we cannot say that building a heap is heapify. It’s just an essential part of the process.